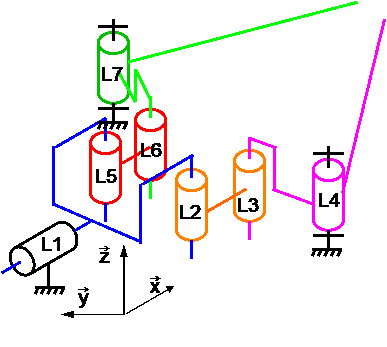On change les liaisons L2, L3, L5, L6 par des pivot glissant pour laisser les biellettes libres de se positionner axialement.

Détermination du degré d'hyperstatisme:

h=m+6µ-Ic avec m le degré de mobilité: ici il n'y a qu'une mobilité utile mu=1 et deux mobilités internes (la translation de chaque biellettes suivant Z) mi=2 d'ou m=3

le nombre de cycle indépendant µ = N_L - N_P +1, ici j'ai N_L= 7 liaisons et N_P= 6 solides d'où µ = 2

et pour finir les inconnues cinématiques pour chaque liaisons: (L1): 2 inconnues (L2): 2 inconnues (L3): 2 inconnues (L4): 1 inconnue (L5): 2 inconnues (L6): 2 inconnues et (L7): 1 inconnue d'où Ic=12 soit h=3+(6×2)-12

h=3 Le degré d'hyperstatisme de cette shématisation spatiale est de 3. Par rapport à ma modélisation précédent, nous avons levé deux degrés d'hyperstatisme (contrainte de positionnement axial suivant Z des biellettes) mais cela reste insuffisant.

Hypothèse simplificatrice: le système présente une sysmétrie géométrique, ainsi qu'une sysmétrie supposée des efforts. Nous modélisons le système que sur une moitié.

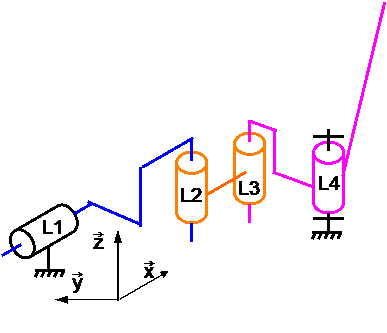
 h=m+6µ-Ic avec m le degré de mobilité: ici il n'y a qu'une mobilité utile mu=1 et une mobilité interne mi=1 d'où m=2

le nombre de cycle indépendant µ = N_L - N_P +1, ici j'ai N_L= 4 liaisons et N_P= 4 solides d'où µ = 1

et pour finir les inconnues cinématiques pour chaque liaisons: (L1): 2 inconnues (L2): 2 inconnues (L3): 2 inconnues (L4): 1 inconnue d'où Ic=7 soit h=2+(6×1)-7

h=1 Le degré d'hyperstatisme de cette shématisation spatiale est de 1.